1. Oldjuk meg a következő egyenletrendszert a valós számok hal­mazán!
   

2. Egy óra számlapja 20 cm oldalhosszúságú szabályos háromszög. A mutatókat a háromszög középpontjában rögzítették úgy, hogy 12 óra­kor az egyik csúcs felé mutatnak. Adjuk meg a nagymutató hosszának legnagyobb értékét, ha a nagymutató nem nyúlik túl az óra számlapján.

3. Az A-ból B-be elindult egy biciklis és ugyanakkor indult el B-ből A-ba egy gyalogos is. Mind a ketten állandó nagyságú sebességgel haladtak. Amikor a biciklis B-be ért, a gyalogos még csak az útja ötöd­részét tette meg. Ha a biciklis 10 km/h-val kisebb, a gyalogos 3 km/h-val nagyobb sebességgel haladt volna, akkor a biciklis célba érésekor a gyalogos az útja háromötöd részét tette volna meg. Mekkora a biciklis és a gyalogos sebessége?

4. Igazolja, hogy a következő kifejezés minden pozitív egész esetén osztható 2015-tel! .

5. Hat darab A és hét darab B betűből készítünk betűsorokat a betűk egymás mellé írásával. Hány olyan betűsort tudunk készíteni, amely palindrom, azaz oda-vissza olvasva ugyanaz?

1. Bizonyítsa be, hogy egy 4 fős társaságban mindig akad két ember, akinek ugyanannyi ismerőse van a társaságban levők között. (Az ismeretséget kölcsönösnek tekintjük.)

2. Egy kétjegyű szám 18-cal nagyobb annál a számnál, melyet úgy ka­punk, hogy a számjegyeit felcseréljük; és -szor nagyobb, mint a számjegyeinek szorzata. Melyik ez a szám?

3. Válasszuk ki az 50 cm kerületű, egyenlő szárú háromszögek közül azt, amelyben minimális az oldalakra rajzolható négyzetek terület­összege.

4. Igazolja, hogy egy kocka oldaléle, lapátlója és testátlója felhasználásával készített háromszög derékszögű; és ennek a háromszögnek valamelyik két súlyvonala merőleges egymásra!

5. Határozzuk meg a következő kifejezés értelmezési tartományát!
   .

1. Egy sakkversenyen mindenki mindenki mással pontosan egy mérkő­zést játszik. Eddig 25 partit fejeztek be, és még mindenkinek hátra van négy partija. Hány sakkozó vesz részt a versenyen?

2. Mutassuk meg, hogy a
   
   kifejezés értéke x-től független ().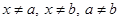

3. Az ABC derékszögű háromszög AB átfogója egységnyi. A-nál fekvő szöge 30°, súlypontja S. Mekkora részekre bontja a BC befogót a BSC szög szögfelezője?

4. Egy kövezeten 10 cm oldalhosszúságú szabályos hatszögekből álló rajzolat van. A padlóra véletlenszerűen 200 Ft-os érmét dobunk, melynek sugara 1,6 cm. Mennyi a valószínűsége, hogy az érme vo­nalat érve helyezkedik el?

5. Ábrázolja az függvényt az intervallu­mon! Tekintsük egyenletet, ahol p paraméter. Vizsgálja a megoldások számát a p paraméter függvényében!

1. Oldjuk meg a valós számok halmazán az alábbi egyenletet:
   

2. Az sorozat a következőképpen van megadva: és minden egész számra. Igazoljuk, hogy az sorozat minden tagja egész szám

3. Adott síkot érint négy R sugarú gömb úgy, hogy középpontjaik egy négyzet 4 csúcsába esnek és a szomszédos gömbök érintik egymást. Egy ötödik gömb érinti mind a négy gömböt és a síkot. Határozzuk meg ezen ötödik gömb sugarát!

4. Határozzuk meg az
   
   függvény legkisebb értékét az intervallumon!

5. Egy háromszög oldalai a, b, c. Mekkora a valószínűsége, hogy egy tetszőleges pontot véletlenszerűen kiválasztva a háromszög belsejé­ben az a c oldalhoz lesz a legközelebb?

Szakközépiskola I.

1. ?
2. ?
3. ?
4. ?
5. ?

Szakközépiskola II.

1. ?
2. ?
3. ?
4. ?
5. ?

Gimnázium I.

1. ?
2. ?
3. ?
4. ?
5. ?

Gimnázium II.

1. ?
2. ?
3. ?
4. ?
5. ?