|
|
2004. február 28.
Pálffy Miklós Kereskedelmi Szakközépiskola, Győr
Három (pozitív) prímszám szorzata egyenlő számtani közepük huszonegyszeresével. Melyek ezek a prímek.
Bizonyítsa be, hogy  osztható 10-zel. osztható 10-zel.
Legyen n kettőnél nagyobb természetes szám. Határozza meg az 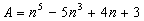 kifejezés utolsó számjegyét. kifejezés utolsó számjegyét.
Egy szimmetrikus trapéz átlói merőlegesek egymásra és 1:7 arányban osztják egymást. Mekkora a trapéz területe, ha kerülete 
Egy urnában 3 fekete, 2 fehér és 4 sárga golyó van. Egymás után, visszatevés nélkül kihúzunk kettőt. Mekkora az esélye annak, hogy mind a kettő fekete.
|
Hány olyan ötjegyű szám van, amelyben minden előforduló számjegy annyiszor szerepel, mint amennyi a számjegy értéke.
Melyik az a két szabályos sokszög, amelyek szögei nagyságának aránya megegyezik csúcsaik számának arányával.
Egy háromszög T területére teljesül, hogy  . Mekkora a c oldallal szemközti szög. . Mekkora a c oldallal szemközti szög.
Három fiú golyókkal játszik. A játék előtt golyóik aránya 7:6:5, játék után 6:5:4.Egyikük 12 golyót nyert. Hány golyójuk volt külön-külön a játék előtt.
Egy 12 dm hosszú, 8 dm széles téglalap alakú üvegtábla egyik sarkából letörött egy 3dm és 4 dm hosszúságú befogókkal rendelkező derékszögű háromszög alakú darab. A megmaradó részből kivágtuk (az eredeti oldalakkal párhuzamosan) a lehető legnagyobb területű téglalap alakú táblát. Mekkorák ennek az oldalai.
|
Melyik az a tíz különböző pozitív egész szám, amelyek összege 56?
Az ABCD konvex négyszögnek A-nál 60o-os, B-nél és D-nél pedig derékszöge van, továbbá AD = 12 egység. A D csúcsnak az AB oldalon levő merőleges vetülete felezi az AB oldalt. Mekkora a négyszög területe?
Határozd meg az összes olyan p prímszámot, amelyre p2+8 is prímszám!
Egy háromszög beírt körének középpontját tükrözzük az oldalakra. Mekkora a háromszög A csúcsnál levő szöge, ha a tükörképeken átmenő kör tartalmazza az A csúcsot?
|
Oldjuk meg a való számok halmazán a következő egyenletet:
 ! !
Definiáljuk a valós számok halmazán az alábbi két művelet:  és és  . Határozd meg a sík azon P(x;y) pontjainak halmazát, amelyekre . Határozd meg a sík azon P(x;y) pontjainak halmazát, amelyekre  és és 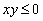 ! !
Legyen adott az ABC háromszög. Rajzoljunk a háromszög beírt köréhez az egyik oldallal párhuzamos érintőt. Bizonyítsuk be, hogy az érintő háromszögön belüli szakasza nem nagyobb, mint a kerület nyolcadrésze!
Bizonyítsuk be, hogy nincs olyan (x,y,z) számhármas, amelyre az  kifejezés minden valós a, b és c értékre nullával lenne egyenlő! kifejezés minden valós a, b és c értékre nullával lenne egyenlő!
|
Szakközépiskola I.
- Rigó József
Deák Ferenc Közgazdasági Szakközépiskola
- Neuberger Etelka
Porpáczy Aladár Kertészeti Szakközépiskola
- Tűz Csaba
Jedlik Ányos Gépipari és Informatikai Középiskola
- Schall Barbara
Deák Ferenc Közgazdasági Szakközépiskola
- Fekete Krisztián
Jedlik Ányos Gépipari és Informatikai Középiskola
Szakközépiskola II.
- Balázs Miklós
Jedlik Ányos Gépipari és Informatikai Középiskola
- Tóth Krisztián
Vas és Villamosipari Szakképző Iskola és Gimnázium
- (Megosztott díj)
Horváth Ágnes Erika
Fáy András Közgazdasági Szakközépiskola
Kiss József
Pattantyús Ábrahám Géza Ipari Szakközépiskola
- (Megosztott díj)
Horváth Miklós
Vas és Villamosipari Szakképző Iskola és Gimnázium
Szabó Diána Nóra
Gimnázium I.
- (Megosztott díj)
Nikházy László
Kazinczy Ferenc Gimnázium
Csorba János
Apor Vilmos Katolikus Iskolaközpont
Estélyi István
Kodály Zoltán Gimnázium, Galánta
Csató László
Révai MIklós Gimnázium
Antal Máté
Révai MIklós Gimnázium
Különdíj
Páldy Sándor
Kodály Zoltán Gimnázium, Galánta
Gimnázium II.
- Birkus Róbert
Kodály Zoltán Gimnázium, Galánta
- Pathó Róbert
Párkányi 8 osztályos Gimnázium
- (Megosztott díj)
Dömötör Erika
Révai Miklós Gimnázium
Stippinger Marcell
Széchenyi István Gimnázium
- Pathó Gábor
Párkányi 8 osztályos Gimnázium
Különdíj
Pál Gyula
Rimaszombat
|
|






 osztható 10-zel.
osztható 10-zel.
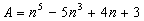 kifejezés utolsó számjegyét.
kifejezés utolsó számjegyét.

 . Mekkora a c oldallal szemközti szög.
. Mekkora a c oldallal szemközti szög.
 !
!
 és
és  . Határozd meg a sík azon P(x;y) pontjainak halmazát, amelyekre
. Határozd meg a sík azon P(x;y) pontjainak halmazát, amelyekre  és
és 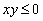 !
!
 kifejezés minden valós a, b és c értékre nullával lenne egyenlő!
kifejezés minden valós a, b és c értékre nullával lenne egyenlő!
































